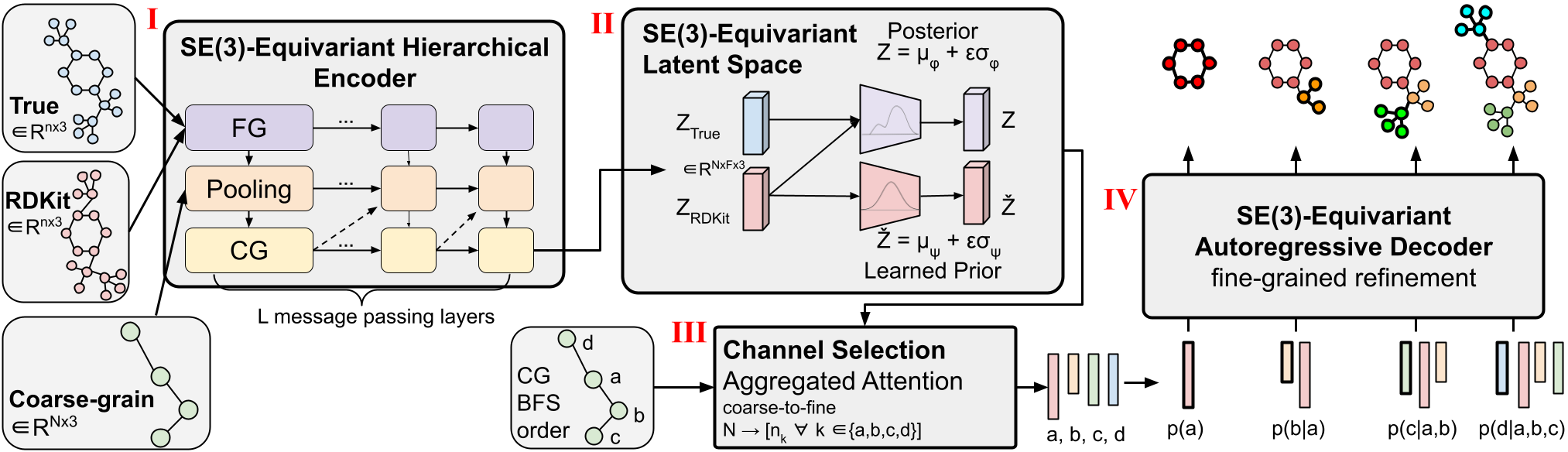
Рисунок 1: Архитектура CoarsenConf.
Генерация молекулярных конформеров является фундаментальной задачей вычислительной химии. Цель состоит в том, чтобы предсказать стабильные низкоэнергетические трехмерные молекулярные структуры, известные как конформеры, с учетом двумерной молекулы. Точные молекулярные конформации имеют решающее значение для различных приложений, которые зависят от точных пространственных и геометрических качеств, включая открытие лекарств и стыковку белков.
Мы представляем CoarsenConf, SE(3)-эквивариантный иерархический вариационный автокодировщик (VAE), который объединяет информацию из мелкозернистых координат атомов в крупнозернистое представление на уровне подграфа для эффективной генерации авторегрессионного конформера.
Фон
Грубое измельчение уменьшает размерность задачи, позволяя генерировать условную авторегрессию, а не генерировать все координаты независимо, как это делалось в предыдущей работе. Путем непосредственного учета трехмерных координат ранее сгенерированных подграфов наша модель лучше обобщает химически и пространственно схожие подграфы. Это имитирует лежащий в основе процесс молекулярного синтеза, когда небольшие функциональные единицы соединяются вместе, образуя большие молекулы, подобные лекарству. В отличие от предыдущих методов, CoarsenConf генерирует низкоэнергетические конформеры с возможностью прямого моделирования координат атомов, расстояний и углов скручивания.
Архитектуру CoarsenConf можно разбить на следующие компоненты:
(Я) Кодер $q_\phi(z| X, \mathcal{R})$ принимает мелкозернистый (FG) основной конформер $X$, приближенный конформер RDKit $\mathcal{R}$ и крупнозернистый (CG ) конформер $\mathcal{C}$ в качестве входных данных (полученный из $X$ и предопределенной стратегии CG) и выводит эквивариантное представление CG переменной длины посредством эквивариантной передачи сообщений и точечных сверток.
(II) Эквивариантные MLP применяются для изучения среднего и логарифмического отклонения как апостериорного, так и априорного распределений.
(III) Апостериорное (обучение) или априорное (вывод) отбирается и передается в модуль выбора канала, где уровень внимания используется для изучения оптимального пути от структуры CG к структуре FG.
(IV) Учитывая латентный вектор ФГ и приближение RDKit, декодер $p_\theta(X |\mathcal{R}, z)$ учится восстанавливать низкоэнергетическую структуру ФГ посредством авторегрессионной эквивариантной передачи сообщений. Вся модель может быть обучена сквозным путем оптимизации KL-расхождения скрытых распределений и ошибки реконструкции сгенерированных конформеров.
Формализм задачи MCG
Мы формализуем задачу генерации молекулярных конформеров (MCG) как моделирование условного распределения $p(X|\mathcal{R})$, где $\mathcal{R}$ — приближенный конформер, сгенерированный RDKit, а $X$ — оптимальный низкоэнергетические конформеры. RDKit, широко используемая библиотека хеминформатики, использует дешевый алгоритм, основанный на геометрии расстояния, за которым следует недорогая оптимизация, основанная на физике, для достижения разумных аппроксимаций конформеров.
Крупнозернистый
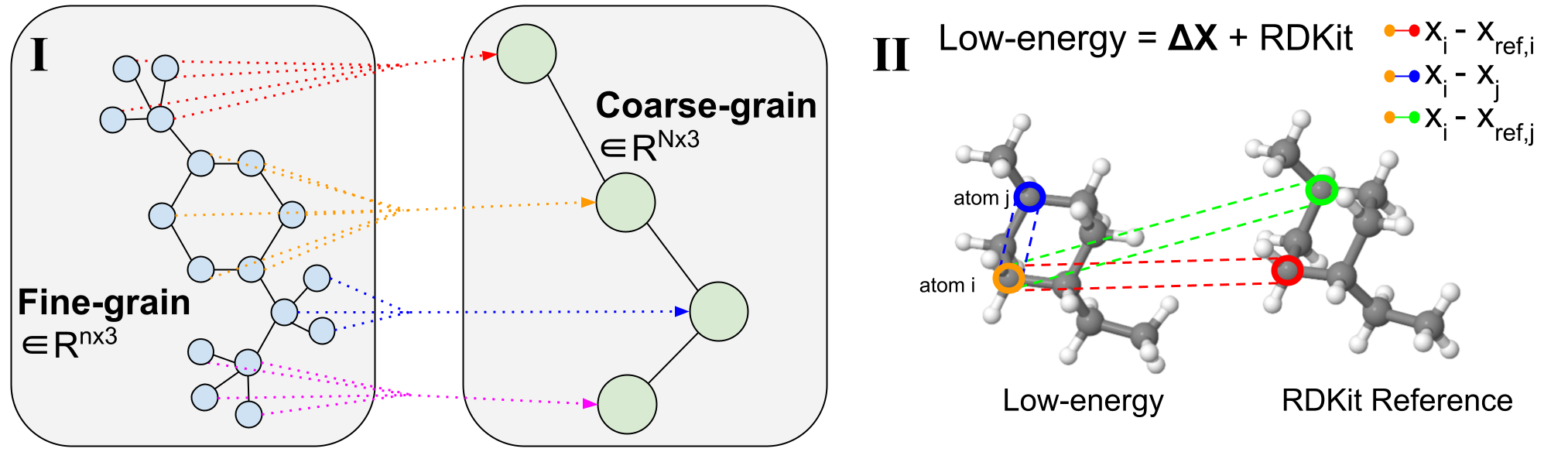
Рисунок 2: Процедура грубого анализа.
(Я) Пример грубого анализа переменной длины. Мелкозернистые молекулы расщепляются по вращающимся связям, которые определяют торсионные углы. Затем они детализируются, чтобы уменьшить размерность и изучить скрытое распределение на уровне подграфа. (II) Визуализация 3D-конформера. Конкретные пары атомов выделяются для операций передачи сообщений декодера.
Молекулярная грубая обработка упрощает представление молекулы путем группировки мелкозернистых (FG) атомов исходной структуры в отдельные крупнозернистые (CG) шарики $\mathcal{B}$ с отображением на основе правил, как показано на рисунке 2. (Я). Грубое зернообразование широко используется в белковом и молекулярном дизайне, и, аналогично, генерация на уровне фрагментов или подграфов оказалась очень ценной в различных задачах двухмерного проектирования молекул. Разбиение генеративных задач на более мелкие части — это подход, который можно применить к нескольким задачам, связанным с трехмерными молекулами, и он обеспечивает естественное уменьшение размерности, что позволяет работать с большими сложными системами.
Мы отмечаем, что по сравнению с предыдущими работами, в которых основное внимание уделяется стратегиям CG фиксированной длины, где каждая молекула представлена с фиксированным разрешением $N$ CG шариков, наш метод использует CG переменной длины из-за его гибкости и способности поддерживать любой выбор грубых граней. техника зернения. Это означает, что одна модель CoarsenConf может быть обобщена до любого грубого разрешения, поскольку входные молекулы могут сопоставляться с любым количеством шариков CG. В нашем случае атомы, входящие в состав каждого связного компонента, образующегося в результате разрыва всех вращающихся связей, сгущаются в единую бусину. Этот выбор в процедуре компьютерной графики неявно заставляет модель изучать углы скручивания, а также координаты атомов и межатомные расстояния. В наших экспериментах мы используем GEOM-QM9 и GEOM-DRUGS, которые в среднем содержат 11 атомов и 3 шарика CG и 44 атома и 9 шариков CG соответственно.
SE(3)-эквивариантность
Ключевым аспектом при работе с 3D-структурами является поддержание соответствующей эквивалентности. Трехмерные молекулы эквивариантны относительно вращений и трансляций, или SE(3)-эквивариантности. Мы применяем SE(3)-эквивариантность в кодере, декодере и скрытом пространстве нашей вероятностной модели CoarsenConf. В результате $p(X | \mathcal{R})$ остаётся неизменным при любом ротационном перемещении приближенного конформера $\mathcal{R}$. Более того, если $\mathcal{R}$ повернуть по часовой стрелке на 90°, мы ожидаем, что оптимальный $X$ продемонстрирует такое же вращение. Подробное определение и обсуждение методов поддержания эквивариантности см. в полной версии статьи.
Совокупное внимание
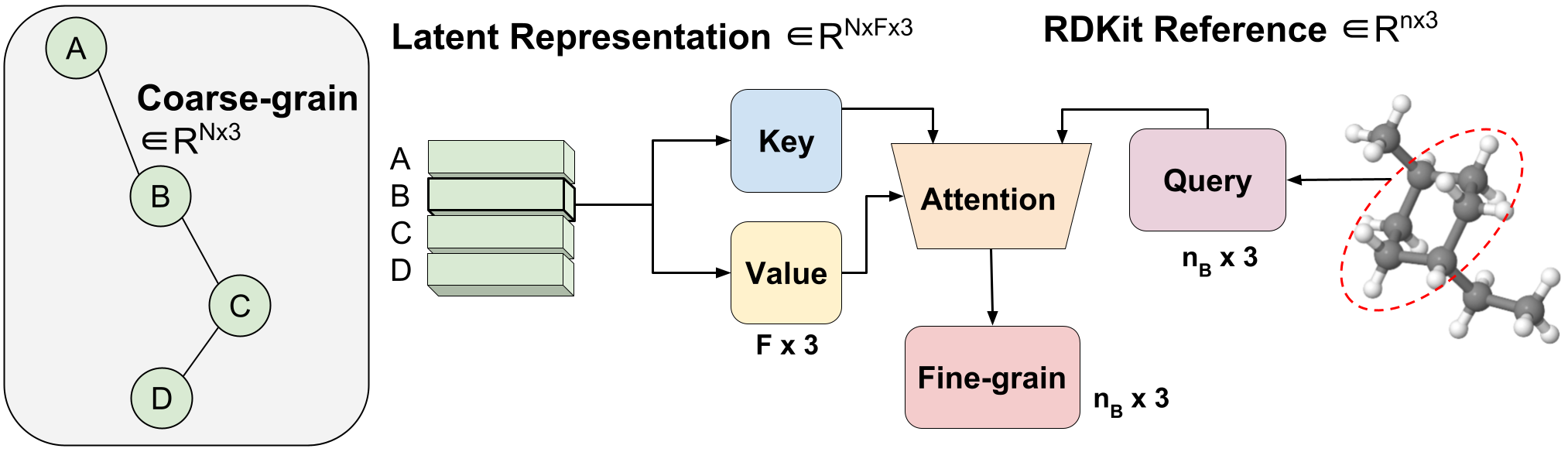
Рис. 3. Обратное отображение переменной длины от грубого к мелкому с помощью агрегированного внимания.
Мы вводим метод, который мы называем «Агрегированное внимание», для изучения оптимального отображения переменной длины из скрытого представления ЦТ в координаты ФГ. Это операция переменной длины, поскольку одна молекула с $n$ атомами может сопоставляться с любым количеством $N$ бусинок CG (каждая бусинка представлена одним скрытым вектором). Скрытый вектор одной бусины CG $Z_{B}$ $\in R^{F \times 3}$ используется в качестве ключа и значения одной операции внимания головы с размером встраивания, равным трем, для соответствия x, координаты y, z. Вектор запроса — это подмножество конформера RDKit, соответствующего шарику $B$ $\in R^{ n_{B} \times 3}$, где $n_B$ — переменная длина, поскольку мы априори знаем, сколько атомов FG соответствует к определенному шарику CG. Используя внимание, мы эффективно изучаем оптимальное сочетание скрытых функций для реконструкции FG. Мы называем это агрегированным вниманием, потому что оно объединяет трехмерные сегменты информации FG для формирования нашего скрытого запроса. Агрегированное внимание отвечает за эффективный перевод скрытого представления ЦТ в жизнеспособные координаты ФГ (рис. 1(III)).
Модель
CoarsenConf — это иерархический VAE с SE(3)-эквивариантным кодером и декодером. Кодер работает с SE(3)-инвариантными атомными координатами $h \in R^{ n \times D}$ и SE(3)-эквивариантными атомистическими координатами $x \in R^{n \times 3}$. Одиночный уровень кодировщика состоит из трех модулей: мелкозернистого, пула и крупнозернистого. Полные уравнения для каждого модуля можно найти в полной статье. Кодировщик создает окончательный эквивариантный тензор CG $Z \in R^{N \times F \times 3}$, где $N$ — количество бусинок, а F — определяемый пользователем скрытый размер.
Роль декодера двоякая. Первый — преобразовать скрытое огрубленное представление обратно в пространство FG посредством процесса, который мы называем выбором канала и который использует агрегированное внимание. Второй — уточнить мелкозернистое представление авторегрессией для получения окончательных низкоэнергетических координат (рис. 1 (IV)).
Мы подчеркиваем, что за счет грубой настройки за счет связности углов скручивания наша модель изучает оптимальные углы скручивания неконтролируемым образом, поскольку условные входные данные в декодер не выровнены. CoarsenConf обеспечивает правильный поворот каждого следующего сгенерированного подграфа для достижения низкой ошибки координат и расстояния.
Результаты эксперимента
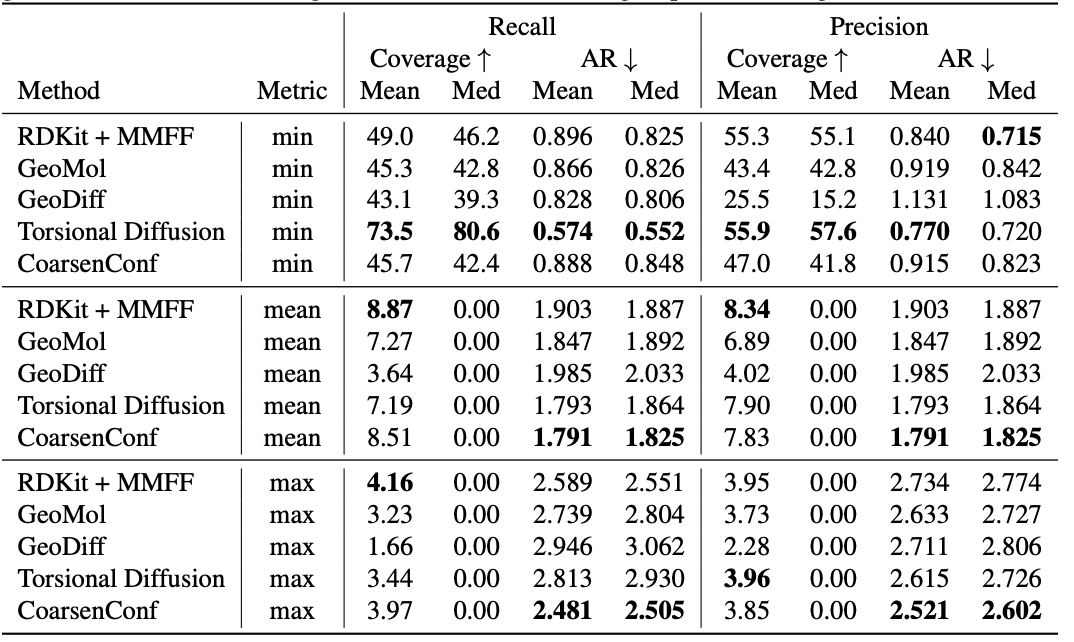
Таблица 1: Качество сгенерированных ансамблей конформеров для тестового набора GEOM-DRUGS ($\delta=0,75Å$) с точки зрения охвата (%) и среднего RMSD ($Å$). CoarsenConf (5 эпох) был ограничен использованием 7,3% данных, использованных Torsional Diffusion (250 эпох), чтобы проиллюстрировать режим с низким уровнем вычислений и ограничением данных.
Средняя ошибка (AR) является ключевым показателем, который измеряет среднее RMSD для сгенерированных молекул соответствующего набора тестов. Покрытие измеряет процент молекул, которые могут быть сгенерированы в пределах определенного порога ошибки ($\delta$). Мы вводим средние и максимальные метрики, чтобы лучше оценить устойчивую генерацию и избежать систематической ошибки выборки минимальной метрики. Мы подчеркиваем, что минимальная метрика дает неосязаемые результаты, поскольку, пока оптимальный конформер не известен априори, невозможно узнать, какой из конформеров, сгенерированных 2L для отдельной молекулы, является лучшим. В таблице 1 показано, что CoarsenConf генерирует наименьшую среднюю и наихудшую ошибку по всему тестовому набору молекул ЛЕКАРСТВ. Мы также показываем, что RDKit с недорогой оптимизацией на основе физики (MMFF) обеспечивает лучший охват, чем большинство методов, основанных на глубоком обучении. Формальные определения показателей и дальнейшее обсуждение см. в полном документе, ссылка на который приведена ниже.
Более подробную информацию о CoarsenConf можно найти в статье на arXiv.
БибТекс
Если CoarsenConf вдохновляет вашу работу, процитируйте ее:
@article{reidenbach2023coarsenconf,
title={CoarsenConf: Equivariant Coarsening with Aggregated Attention for Molecular Conformer Generation},
author={Danny Reidenbach and Aditi S. Krishnapriyan},
journal={arXiv preprint arXiv:2306.14852},
year={2023},
}
