Рисунок 1: поэтапное поведение при самостоятельном обучении. При обучении общих алгоритмов SSL мы обнаруживаем, что потери ступенчато уменьшаются (вверху слева), а размерность изученных вложений итеративно увеличивается (внизу слева). Прямая визуализация вложений (справа; показаны три верхних направления PCA) подтверждает, что вложения изначально сжимаются в точку, которая затем расширяется до 1D-многообразия, 2D-многообразия и далее одновременно с этапами потери.
Широко распространено мнение, что ошеломляющий успех глубокого обучения отчасти обусловлен его способностью обнаруживать и извлекать полезные представления сложных данных. Самоконтролируемое обучение (SSL) стало ведущей основой для изучения этих представлений изображений непосредственно из неразмеченных данных, аналогично тому, как студенты LLM изучают представления языка непосредственно из текста, извлеченного из Интернета. Тем не менее, несмотря на ключевую роль SSL в современных моделях, таких как CLIP и MidJourney, фундаментальные вопросы, такие как «что на самом деле изучают системы изображений с самоконтролем?» и «как на самом деле происходит это обучение?» не хватает элементарных ответов.
В нашей недавней статье (которая появится на ICML 2023) мы предлагаем следующее: первая убедительная математическая картина процесса обучения крупномасштабным методам SSL. Наша упрощенная теоретическая модель, которую мы решаем точно, изучает аспекты данных в виде серии дискретных, хорошо разделенных шагов. Затем мы демонстрируем, что такое поведение можно наблюдать в природе во многих современных системах. Это открытие открывает новые возможности для улучшения методов SSL и позволяет задать целый ряд новых научных вопросов, ответы на которые предоставят мощную линзу для понимания некоторых из наиболее важных современных систем глубокого обучения.
Фон
Здесь мы сосредоточимся на методах совместного внедрения SSL — расширенном наборе контрастных методов — которые изучают представления, подчиняющиеся критериям инвариантности представления. Функция потерь этих моделей включает член, обеспечивающий соответствие вложений для семантически эквивалентных «представлений» изображения. Примечательно, что этот простой подход дает мощное представление о задачах с изображениями, даже если представления такие же простые, как случайное кадрирование и искажения цвета.
Теория: поэтапное обучение SSL с линеаризованными моделями
Сначала мы описываем точно решаемую линейную модель SSL, в которой как траектории обучения, так и окончательные вложения могут быть записаны в замкнутой форме. Примечательно, что мы обнаружили, что обучение представлению разделяется на ряд дискретных шагов: ранг вложений начинается с малого и итеративно увеличивается в пошаговом процессе обучения.
Основной теоретический вклад нашей статьи заключается в точном решении динамики обучения функции потерь Близнецов Барлоу при градиентном потоке для частного случая линейной модели \(\mathbf{f}(\mathbf{x}) = \mathbf{W } \mathbf{x}\). Подводя итог нашим выводам, мы обнаруживаем, что при небольшой инициализации модель изучает представления, состоящие точно из верхних \(d\) собственных направлений характерно матрица взаимной корреляции \(\boldsymbol{\Gamma} \equiv \mathbb{E}_{\mathbf{x},\mathbf{x}’} [ \mathbf{x} \mathbf{x}’^T ]\). Более того, мы обнаруживаем, что эти собственные направления изучаются один за раз в последовательности дискретных шагов обучения в моменты времени, определяемые их соответствующими собственными значениями. Рисунок 2 иллюстрирует этот процесс обучения, показывая как рост нового направления представленной функции, так и результирующее падение потерь на каждом этапе обучения. В качестве дополнительного бонуса мы находим уравнение в замкнутой форме для окончательных вложений, изученных моделью при сходимости.
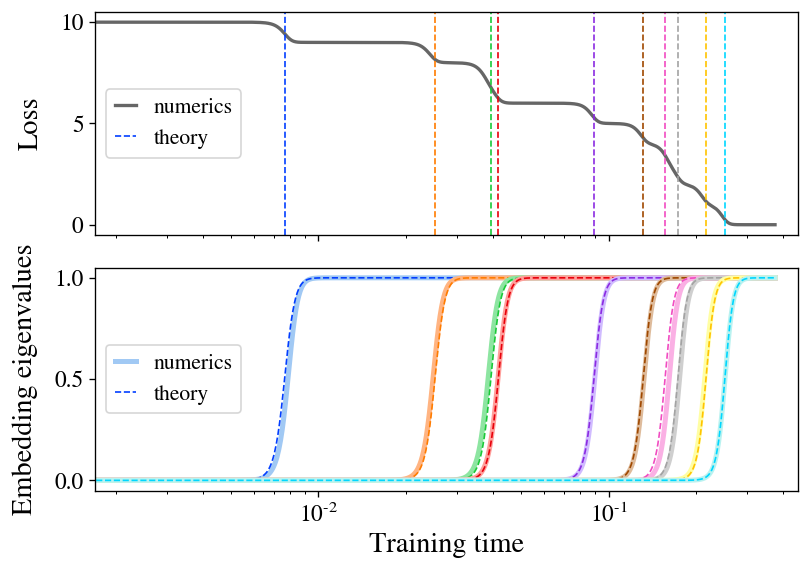
Рисунок 2: поэтапное обучение представлено в линейной модели SSL. Мы обучаем линейную модель с потерей близнецов Барлоу на небольшой выборке CIFAR-10. Потери (вверху) падают по лестнице, время шага хорошо предсказано нашей теорией (пунктирные линии). Собственные значения встраивания (внизу) возникают по одному, что точно соответствует теории (пунктирные кривые).
Наше открытие поэтапного обучения является проявлением более широкой концепции спектральное смещение, что является наблюдением о том, что многие системы обучения с приблизительно линейной динамикой преимущественно изучают собственные направления с более высоким собственным значением. Недавно это было хорошо изучено в случае стандартного обучения с учителем, где было обнаружено, что собственные моды с более высоким собственным значением изучаются быстрее во время обучения. Наша работа дает аналогичные результаты для SSL.
Причина, по которой линейная модель заслуживает тщательного изучения, заключается в том, что, как показано в направлении работы «нейронного касательного ядра» (NTK), достаточно широкие нейронные сети также имеют линейную параметрическую динамику. Этого факта достаточно, чтобы распространить наше решение для линейной модели на широкие нейронные сети (или, по сути, на машины с произвольным ядром), и в этом случае модель преимущественно изучает верхние \(d\) собственные направления конкретного оператора, связанного с NTK. Изучение NTK дало много идей по обучению и обобщению даже нелинейных нейронных сетей, что является ключом к тому, что, возможно, некоторые из полученных нами идей можно перенести на реалистичные случаи.
Эксперимент: поэтапное обучение SSL с помощью ResNets
В качестве наших основных экспериментов мы обучаем несколько ведущих методов SSL с помощью полномасштабных кодировщиков ResNet-50 и обнаруживаем, что, что примечательно, мы четко видим этот шаблон пошагового обучения даже в реалистичных условиях, предполагая, что такое поведение является центральным для поведения обучения SSL.
Чтобы увидеть пошаговое обучение с помощью ResNets в реалистичных условиях, все, что нам нужно сделать, — это запустить алгоритм и отслеживать собственные значения внедряемой ковариационной матрицы с течением времени. На практике это помогает выделить пошаговое поведение, а также обучение с инициализацией параметров, меньших, чем обычно, и обучение с небольшой скоростью обучения, поэтому мы будем использовать эти модификации в экспериментах, о которых мы говорим здесь, и обсудим стандартный случай в наша газета.
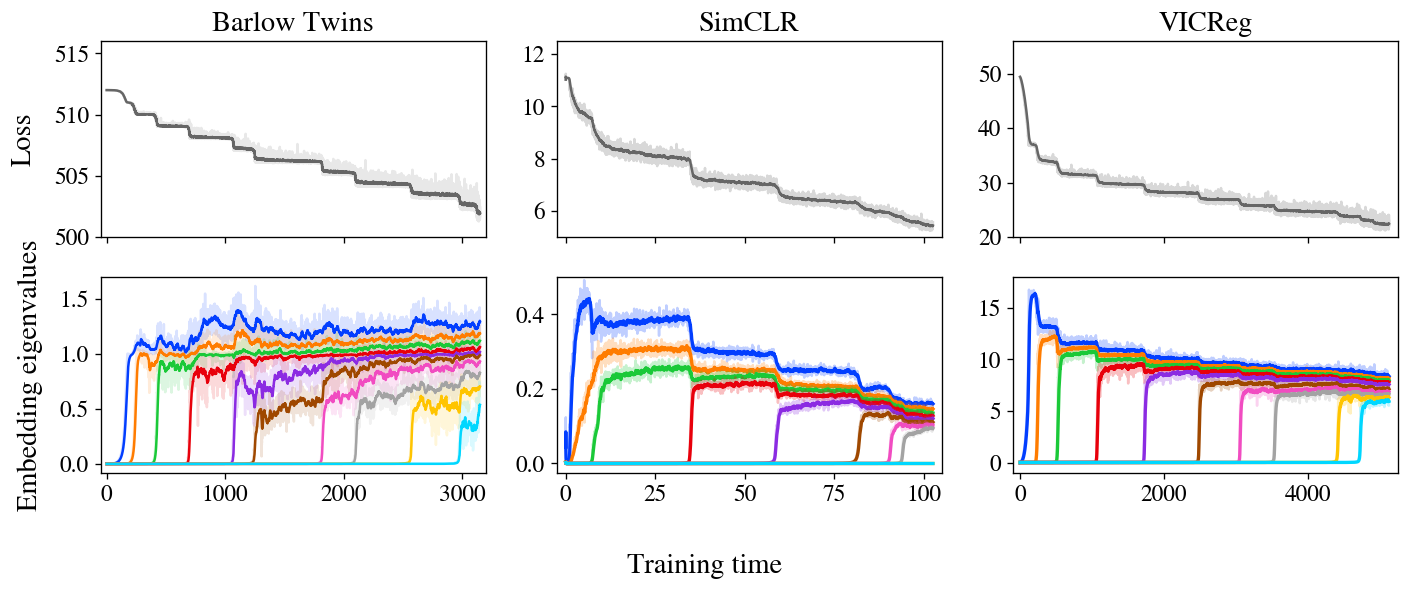
Рисунок 3: поэтапное обучение очевидно в Barlow Twins, SimCLR и VICReg. Потеря и внедрение всех трех методов демонстрируют поэтапное обучение, при этом ранг внедрений итеративно увеличивается, как и предсказывает наша модель.
На рисунке 3 показаны потери и встраивание собственных значений ковариации для трех методов SSL — Barlow Twins, SimCLR и VICReg — обученных на наборе данных STL-10 со стандартными дополнениями. Примечательно, все трое демонстрируют очень четкое поэтапное обучение, с уменьшением потерь по ступенчатой кривой и с одним новым собственным значением, возникающим из нуля на каждом последующем шаге. Мы также показываем в увеличенном масштабе первые шаги «Близнецов Барлоу» на рисунке 1.
Стоит отметить, что, хотя эти три метода на первый взгляд весьма различны, в фольклоре уже некоторое время подозревали, что они делают что-то похожее под капотом. В частности, эти и другие методы совместного внедрения SSL достигают одинаковой производительности в тестовых задачах. Таким образом, задача состоит в том, чтобы определить общее поведение, лежащее в основе этих различных методов. Многие предыдущие теоретические работы были сосредоточены на аналитическом сходстве их функций потерь, но наши эксперименты предполагают другой объединяющий принцип: Все методы SSL изучают встраивания по одному измерению за раз, итеративно добавляя новые измерения в порядке значимости.
В последнем зарождающемся, но многообещающем эксперименте мы сравниваем реальные вложения, полученные с помощью этих методов, с теоретическими предсказаниями, вычисленными на основе NTK после обучения. Мы не только находим хорошее согласие между теорией и экспериментом в рамках каждого метода, но также сравниваем разные методы и обнаруживаем, что разные методы изучают схожие вложения, что добавляет дополнительную поддержку идее о том, что эти методы в конечном итоге делают схожие вещи и могут быть унифицированы.
Почему это важно
Наша работа рисует базовую теоретическую картину процесса, с помощью которого методы SSL собирают изученные представления в ходе обучения. Теперь, когда у нас есть теория, что мы можем с ней сделать? Мы считаем, что эта картина обещает помочь в практике SSL с инженерной точки зрения, а также обеспечить лучшее понимание SSL и, возможно, обучение представлению в более широком смысле.
С практической стороны модели SSL, как известно, обучаются медленнее по сравнению с обучением с учителем, и причина этой разницы неизвестна. Наша картина обучения предполагает, что обучение SSL требует много времени для сходимости, потому что более поздние собственные моды имеют большие постоянные времени и требуют много времени, чтобы значительно вырасти. Если эта картина верна, ускорение обучения было бы так же просто, как избирательное фокусирование градиента на небольших собственных направлениях внедрения в попытке поднять их до уровня остальных, что в принципе можно сделать с помощью простой модификации функции потерь или оптимизатор. Подробнее об этих возможностях мы поговорим в нашей статье.
С научной точки зрения структура SSL как итеративного процесса позволяет задать много вопросов об отдельных собственных модах. Являются ли те, которые выучены первыми, более полезными, чем те, которые выучены позже? Как различные дополнения меняют изученные режимы и зависит ли это от конкретного используемого метода SSL? Можем ли мы присвоить семантическое содержание любому (подмножеству) собственных мод? (Например, мы заметили, что первые несколько изученных режимов иногда представляют собой легко интерпретируемые функции, такие как средний оттенок и насыщенность изображения.) Если другие формы обучения представлениям сходятся к аналогичным представлениям (факт, который легко проверить), тогда ответы на эти вопросы могут иметь последствия, распространяющиеся на глубокое обучение в более широком смысле.
Учитывая все это, мы с оптимизмом смотрим на перспективы будущей работы в этой области. Глубокое обучение остается великой теоретической загадкой, но мы считаем, что наши результаты дают полезную основу для будущих исследований обучающего поведения глубоких сетей.
Этот пост основан на статье «О поэтапной природе самостоятельного обучения», которая является совместной работой с Максисом Кнутиньшем, Лю Цзыином, Даниэлем Гейсом и Джошуа Альбрехтом. Эта работа проводилась совместно с компанией General Intelligent, научным сотрудником которой является Джейми Саймон. Этот пост в блоге размещен здесь. Мы будем рады ответить на ваши вопросы или комментарии.
