В кооперативном многоагентном обучении с подкреплением (MARL) из-за его политика Обычно считается, что методы градиента политик (PG) менее эффективны в отношении выборки, чем методы декомпозиции значений (VD), которые вне политики. Однако некоторые недавние эмпирические исследования показывают, что при правильном представлении входных данных и настройке гиперпараметров мультиагентный PG может достигать удивительно высокой производительности по сравнению с методами VD вне политики.
Почему методы PG могут работать так хорошо? В этом посте мы представим конкретный анализ, чтобы показать, что в определенных сценариях, например, в средах с очень многомодальным ландшафтом вознаграждения, VD может быть проблематичным и привести к нежелательным результатам. Напротив, в этих случаях методы PG с отдельными политиками могут сходиться к оптимальной политике. Кроме того, методы PG с авторегрессивными (AR) политиками могут изучать мультимодальные политики.
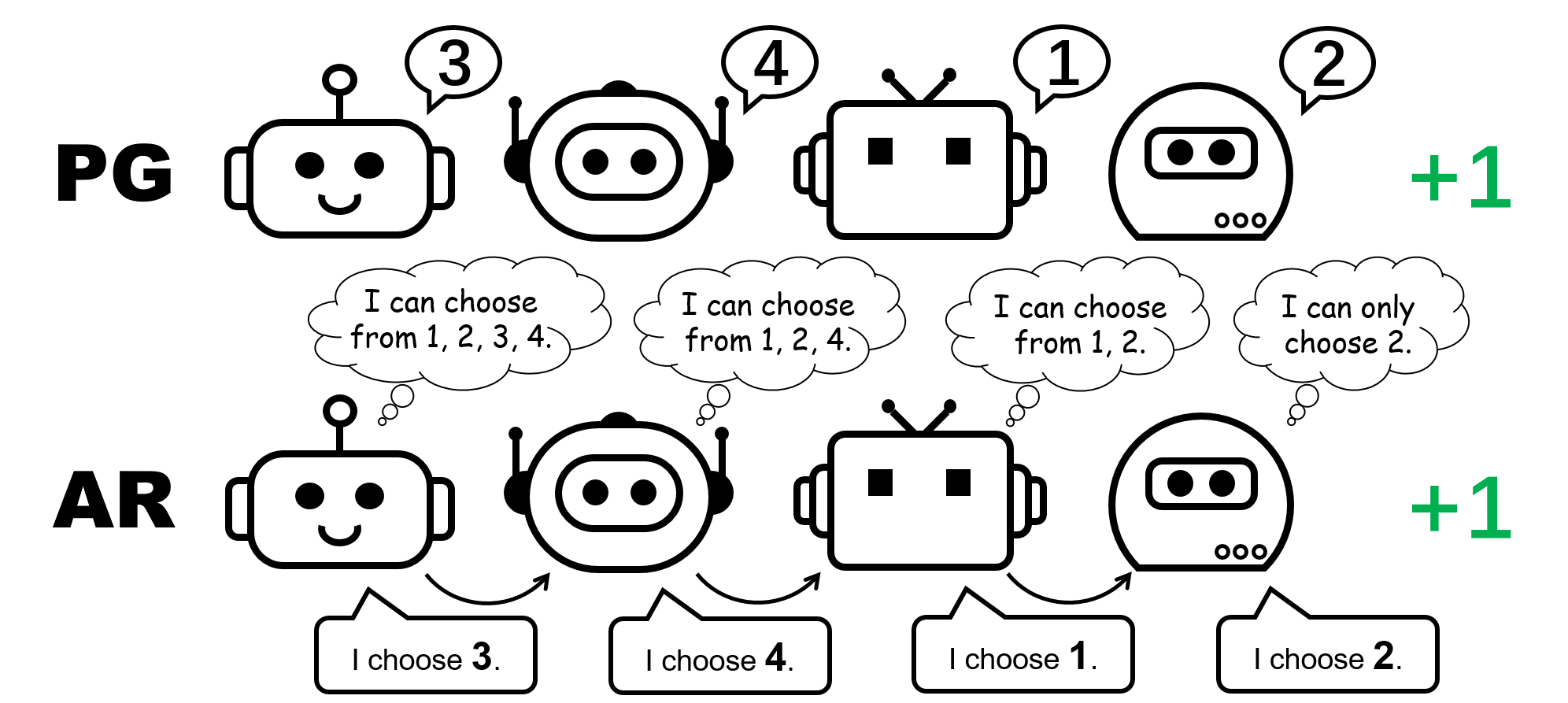
Рисунок 1: другое представление политики для игры с перестановкой для 4 игроков.
CTDE в кооперативном MARL: методы VD и PG
Централизованное обучение и децентрализованное выполнение (CTDE) — популярная структура в кооперативном MARL. Он использует Глобальный информацию для более эффективного обучения при сохранении представления отдельных политик для тестирования. CTDE может быть реализован с помощью декомпозиции значений (VD) или градиента политик (PG), что приводит к двум различным типам алгоритмов.
Методы VD изучают локальные сети Q и функцию смешивания, которая смешивает локальные сети Q с глобальной функцией Q. Функция смешивания обычно применяется для удовлетворения принципа индивидуального глобального максимума (IGM), который гарантирует, что оптимальное совместное действие может быть вычислено путем жадного выбора оптимального действия локально для каждого агента.
Напротив, методы PG напрямую применяют градиент политики для изучения индивидуальной политики и функции централизованного значения для каждого агента. Функция значения принимает в качестве входных данных глобальное состояние (например, MAPPO) или объединение всех локальных наблюдений (например, MADDPG) для точной оценки глобального значения.
Игра в перестановки: простой контрпример, когда VD терпит неудачу
Мы начнем наш анализ с рассмотрения кооперативной игры без состояния, а именно игры перестановок. В перестановочной игре с участием $N$ каждый агент может произвести $N$ действий ${ 1,\ldots, N }$. Агенты получают вознаграждение $+1$, если их действия взаимно различны, т. е. совместное действие представляет собой перестановку над $1, \ldots, N$; в противном случае они получают вознаграждение в размере 0 долларов США. Заметим, что в этой игре существует $N!$ симметричных оптимальных стратегий.
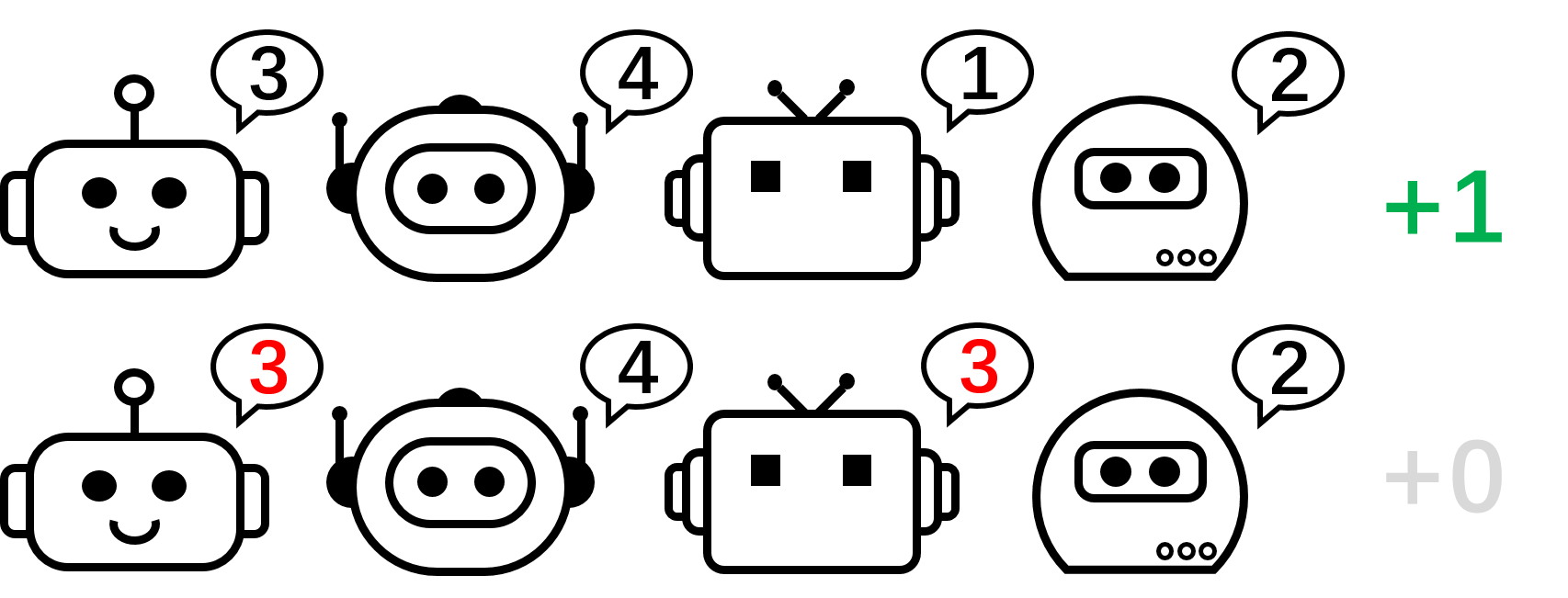
Рисунок 2: игра перестановок для 4 игроков.
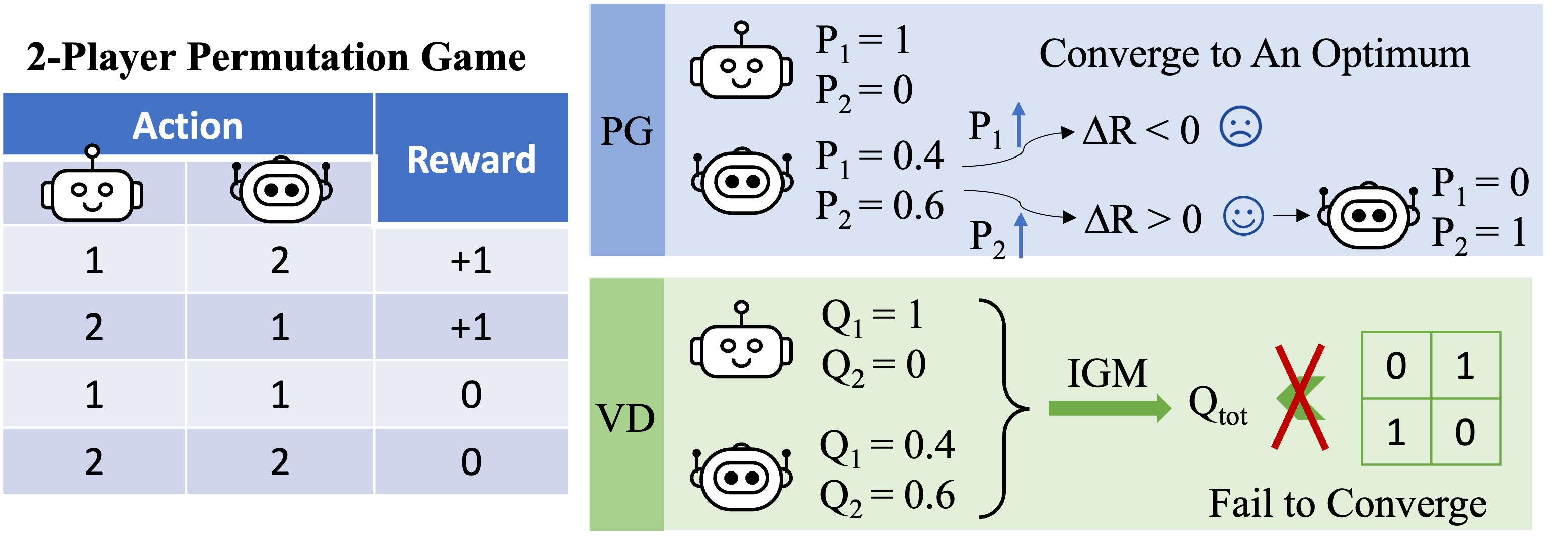
Рисунок 3: Интуитивное представление высокого уровня о том, почему VD терпит неудачу в игре перестановок для двух игроков.
Теперь давайте сосредоточимся на игре с перестановками для двух игроков и применим к ней VD. В этой настройке без сохранения состояния мы используем $Q_1$ и $Q_2$ для обозначения локальных Q-функций и используем $Q_\textrm{tot}$ для обозначения глобальной Q-функции. Принцип IGM требует, чтобы
\[\arg\max_{a^1,a^2}Q_\textrm{tot}(a^1,a^2)=\{\arg\max_{a^1}Q_1(a^1),\arg\max_{a^2}Q_2(a^2)\}.\]
Мы доказываем, что VD не может представлять выигрыш в игре перестановок двух игроков от противного. Если бы методы VD могли представить выигрыш, мы бы имели
\[Q_\textrm{tot}(1, 2)=Q_\textrm{tot}(2,1)=1\quad \text{and}\quad Q_\textrm{tot}(1, 1)=Q_\textrm{tot}(2,2)=0.\]
Если любой из этих двух агентов имеет разные локальные значения Q (например, $Q_1(1)> Q_1(2)$), мы имеем $\arg\max_{a^1}Q_1(a^1)=1$. Тогда по принципу ИГМ любой оптимальное совместное действие
\[(a^{1\star},a^{2\star})=\arg\max_{a^1,a^2}Q_\textrm{tot}(a^1,a^2)=\{\arg\max_{a^1}Q_1(a^1),\arg\max_{a^2}Q_2(a^2)\}\]
удовлетворяет $a^{1\star}=1$ и $a^{1\star}\neq 2$, поэтому совместное действие $(a^1,a^2)=(2,1)$ является суб- оптимальна, т. е. $Q_\textrm{tot}(2,1)<1$.
В противном случае, если $Q_1(1)=Q_1(2)$ и $Q_2(1)=Q_2(2)$, то
\[Q_\textrm{tot}(1, 1)=Q_\textrm{tot}(2,2)=Q_\textrm{tot}(1, 2)=Q_\textrm{tot}(2,1).\]
В результате декомпозиция значений не может представлять матрицу выигрышей игры с перестановками для двух игроков.
А как насчет методов ПГ? Индивидуальные политики действительно могут представлять оптимальную политику для игры перестановок. Более того, стохастический градиентный спуск может гарантировать сходимость PG к одному из этих оптимумов при умеренных предположениях. Это говорит о том, что, хотя методы PG менее популярны в MARL по сравнению с методами VD, они могут быть предпочтительнее в некоторых случаях, которые распространены в реальных приложениях, например, в играх с несколькими модальностями стратегии.
Мы также отмечаем, что в игре перестановок, чтобы представить оптимальную совместную политику, каждый агент должен выбирать различные действия. Следовательно, успешная реализация PG должна гарантировать, что политики зависят от агента. Это можно сделать с помощью либо отдельных политик с неразделяемыми параметрами (называемых в нашей статье PG-Ind), либо политики, обусловленной идентификатором агента (PG-ID).
PG превосходит существующие методы VD на популярных испытательных стендах MARL
Выходя за рамки простого иллюстративного примера игры с перестановками, мы расширяем наше исследование на популярные и более реалистичные тесты MARL. В дополнение к StarCraft Multi-Agent Challenge (SMAC), где была проверена эффективность PG и политики, обусловленной агентами, мы показываем новые результаты в Google Research Football (GRF) и многопользовательском Hanabi Challenge.
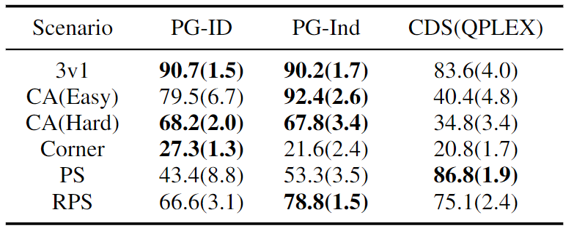
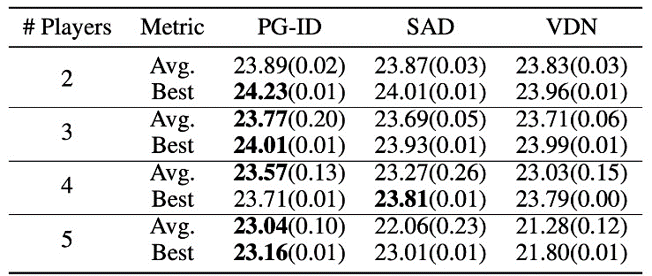
Рисунок 4: (слева) коэффициенты выигрыша методов PG на GRF; (справа) лучшие и средние оценки на Hanabi-Full.
В GRF методы PG превосходят современный базовый уровень VD (CDS) в 5 сценариях. Интересно, что мы также заметили, что отдельные политики (PG-Ind) без совместного использования параметров обеспечивают сопоставимые, а иногда и более высокие показатели выигрыша по сравнению с политиками для конкретных агентов (PG-ID) во всех 5 сценариях. Мы оцениваем PG-ID в полномасштабной игре Hanabi с различным количеством игроков (2-5 игроков) и сравниваем их с SAD, сильным вариантом Q-обучения вне политики в Hanabi и сетями декомпозиции ценности (VDN). Как показано в приведенной выше таблице, PG-ID может давать результаты, сравнимые с лучшими и средними наградами, достигнутыми SAD и VDN, или даже лучше, с разным количеством игроков, использующих одинаковое количество шагов среды.
Помимо более высоких вознаграждений: изучение мультимодального поведения с помощью авторегрессивного моделирования политики
Помимо обучения более высоким вознаграждениям, мы также изучаем, как изучать мультимодальные политики в кооперативном MARL. Вернемся к игре перестановок. Хотя мы доказали, что PG может эффективно обучаться оптимальной политике, режим стратегии, которого он в конечном итоге достигает, может сильно зависеть от инициализации политики. Таким образом, закономерным будет вопрос:
Можем ли мы выучить единую политику, которая может охватывать все оптимальные режимы?
В децентрализованной формулировке PG факторизованное представление совместной политики может представлять только один конкретный режим. Поэтому мы предлагаем расширенный способ параметризации политик для большей выразительности — авторегрессивные (AR) политики.

Рисунок 5: сравнение индивидуальных политик (PG) и авторегрессивных политик (AR) в игре перестановок с 4 игроками.
Формально разложим совместную политику $n$ агентов в виде
\[\pi(\mathbf{a} \mid \mathbf{o}) \approx \prod_{i=1}^n \pi_{\theta^{i}} \left( a^{i}\mid o^{i},a^{1},\ldots,a^{i-1} \right),\]
где действие агента $i$ зависит от его собственного наблюдения $o_i$ и всех действий предыдущих агентов $1,\dots,i-1$. Авторегрессионная факторизация может представлять любой совместная политика в централизованной MDP. только модификация политики каждого агента — это входное измерение, которое немного расширяется за счет включения предыдущих действий; и выходное измерение политики каждого агента остается неизменным.
При таких минимальных затратах на параметризацию политика AR существенно улучшает представление методов PG. Отметим, что PG с политикой AR (PG-AR) может одновременно представлять все оптимальные режимы политики в игре перестановок.

Рисунок: тепловые карты действий для политик, изученных PG-Ind (слева) и PG-AR (в центре), и тепловая карта для вознаграждений (справа); в то время как PG-Ind сходится только к определенному режиму в игре перестановок с 4 игроками, PG-AR успешно обнаруживает все оптимальные режимы.
В более сложных средах, включая SMAC и GRF, PG-AR может изучать интересные эмерджентные модели поведения, требующие сильной координации внутри агента, которые PG-Ind может никогда не изучить.
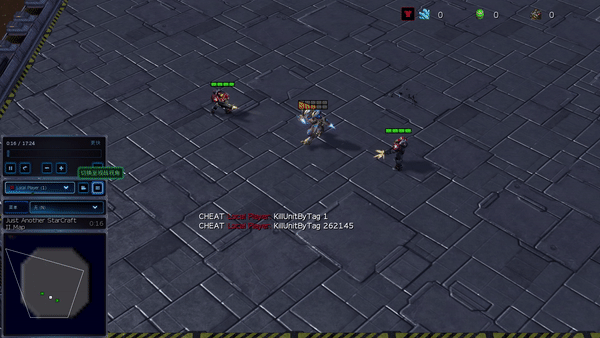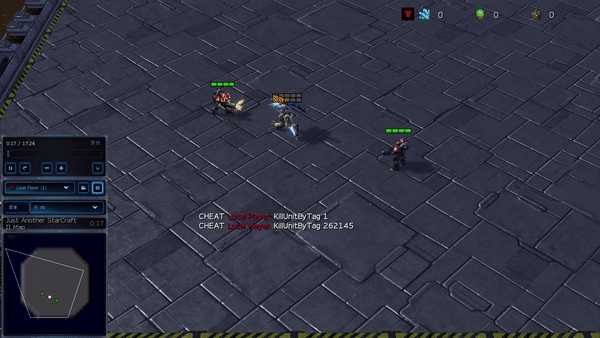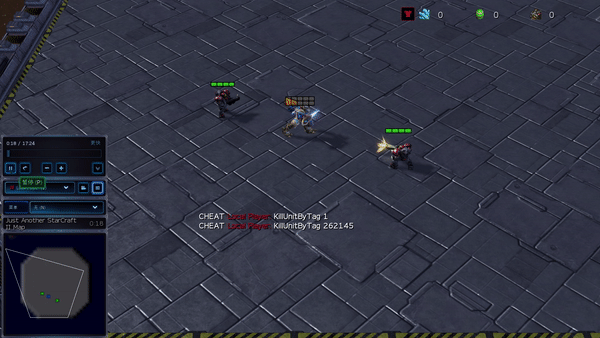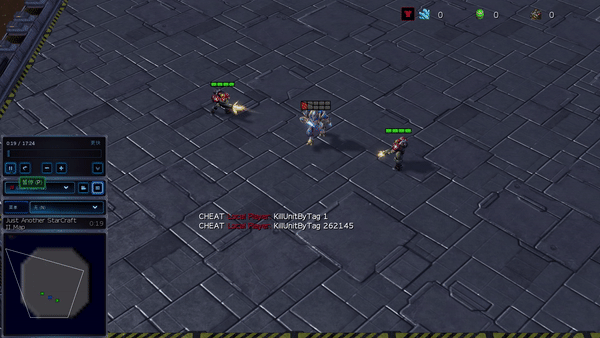
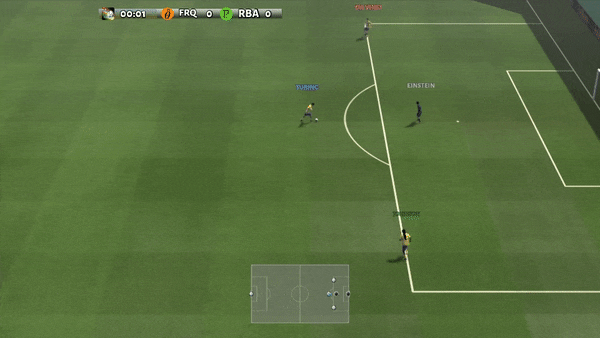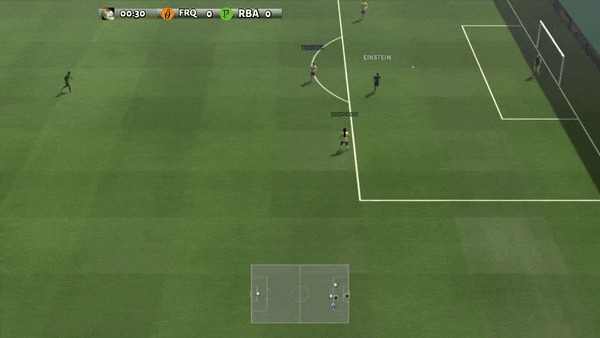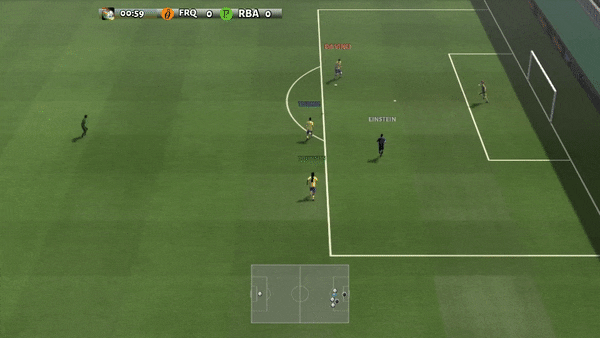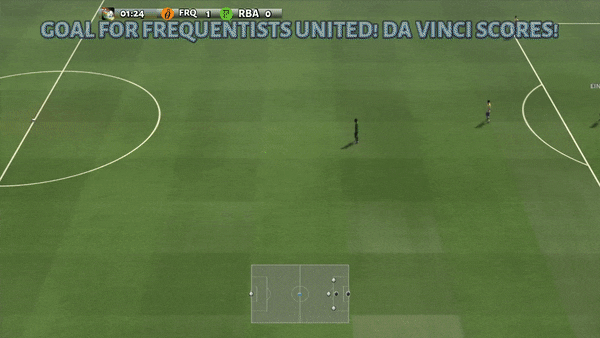
Рисунок 6: (слева) возникающее поведение, вызванное PG-AR в SMAC и GRF. На карте SMAC 2m_vs_1z морские пехотинцы продолжают стоять и атаковать поочередно, при этом гарантируется, что на каждом временном шаге есть только один атакующий морской пехотинец; (справа) в сценарии academy_3_vs_1_with_keeper в GRF агенты учатся поведению в стиле «тики-така»: каждый игрок продолжает передавать мяч своим товарищам по команде.
Обсуждения и выводы
В этом посте мы предоставляем конкретный анализ методов VD и PG в кооперативном MARL. Во-первых, мы раскрываем ограничение выразительности популярных методов VD, показывая, что они не могут представлять оптимальные политики даже в простой игре перестановок. Напротив, мы показываем, что методы PG доказуемо более выразительны. Мы эмпирически проверяем преимущество PG в выразительности на популярных тестовых стендах MARL, включая SMAC, GRF и Hanabi Challenge. Мы надеемся, что выводы из этой работы могут помочь сообществу в создании более общих и более мощных совместных алгоритмов MARL в будущем.
Этот пост основан на нашей статье: «Пересмотр некоторых распространенных практик в совместном многоагентном обучении с подкреплением» (статья, веб-сайт).
